偙偺儁乕僕偵偼丄夋憸偑俁枃娷傑傟偰偄傑偡丅曐懚偟偰偛棙梡偵側傞曽偼丄偛拲堄偔偩偝偄丅
丂嶰暯曽偺掕棟偼丄庡偵乽挿偝乿傪媮傔傞応崌偵巊偆偙偲偺懡偄傕偺偱偡丅
妎偊傞偙偲偼丄偁傑傝偁傝傑偣傫偐傜丄婥帩偪傪妝偵偟偰偍撉傒偔偩偝偄丅
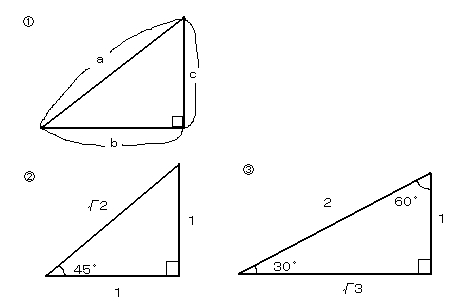
亙嶰暯曽偺掕棟亜
捈妏嶰妏宍偱丄幬曈傪倎丄懠偺俀曈傪倐丄們偲偟偨応崌
嘆倎俀亖倐俀亄們俀丂丂壓恾偺嘆
捈妏嶰妏宍偱丄捈妏埲奜偺妏偑係俆亱偱偁傞応崌
嘇俁偮偺曈偺斾偼丄侾丗侾丗併俀丂丂壓恾偺嘇
捈妏嶰妏宍偱丄捈妏埲奜偺妏偑俁侽亱丄俇侽亱偱偁傞応崌
嘇俁偮偺曈偺斾偼丄侾丗俀丗併俁丂丂壓恾偺嘊
婎杮栤戣墘廗偦偺侾
嘆乣嘍偼丄偡傋偰丄俙俛傪幬曈偲偡傞捈妏嶰妏宍偱偡丅
嘆俙俠亖俁們倣丄俛俠亖係們倣偺偲偒俙俛偺挿偝傪媮傔傛丅
嘇俙俠亖俆們倣丄俛俠亖侾俀們倣偺偲偒丄俙俛偺挿偝傪媮傔傛丅
嘊俙俠亖侾們倣丄俛俠亖俁們倣偺偲偒丄俙俛偺挿偝傪媮傔傛丅
嘋俙俛亖俆併俀們倣丄俛俠亖俈們倣偺偲偒丄俙俠偺挿偝傪媮傔傛丅
嘍俙俛亖俈們倣丄俛俠亖俆們倣偺偲偒丄俙俠偺挿偝傪媮傔傛丅
嘐俀揰乮俀丆俁乯乮俆丆俈乯偺嫍棧傪媮傔傛丅
嘑俀揰乮侾丆係乯乮係丆俈乯偺嫍棧傪媮傔傛丅
夝摎丒夝愢
嘆俙俛亖倃偲偡傞偲丄俙俛偼幬曈偱偡偐傜丄
丂倃俀亖俁俀亄係俀
丂倃俀亖俀俆
丂倃亖亇併俀俆
丂倃亖亇俆
丂倃亖俆乮挿偝側偺偱丄倃亜侽乯
丂摎偊丗俆們倣
嘇俙俛亖倃偲偡傞偲丄俙俛偼幬曈偱偡偐傜丄
丂倃俀亖俆俀亄侾俀俀
丂倃俀亖侾俇俋
丂倃亖亇併侾俇俋
丂倃亖亇侾俁
丂倃亖侾俁乮挿偝側偺偱丄倃亜侽乯
丂摎偊丗侾俁們倣
嘊俙俛亖倃偲偡傞偲丄俙俛偼幬曈偱偡偐傜丄
丂倃俀亖侾俀亄俁俀
丂倃俀亖侾侽
丂倃亖亇併侾侽
丂倃亖併侾侽乮挿偝側偺偱丄倃亜侽乯
丂摎偊丗併侾侽們倣
嘋俙俠亖倃偲偡傞偲丄俙俠偼幬曈偱偼偁傝傑偣傫偐傜丄
丂倃俀亄俈俀亖乮俆併俀乯俀
丂倃俀亖侾
丂倃亖亇併侾
丂倃亖亇侾
丂倃亖侾乮挿偝側偺偱丄倃亜侽乯
丂摎偊丗侾們倣
嘍俙俠亖倃偲偡傞偲丄俙俠偼幬曈偱偼偁傝傑偣傫偐傜丄
丂倃俀亄俆俀亖俈俀
丂倃俀亖俀係
丂倃亖亇併俀係
丂倃亖亇俀併俇
丂倃亖俀併俇乮挿偝側偺偱丄倃亜侽乯
丂摎偊丗俀併俇們倣
嘐俀揰娫偺嫍棧傪倃偲偡傞偲丄
丂倃傪幬曈偲偡傞捈妏嶰妏宍傪峫偊傞偙偲偑偱偒傑偡丅
偙偺応崌丄懠偺俀曈偺挿偝偼丄偦傟偧傟丄
丂倃嵗昗偺嵎丄倄嵗昗偺嵎偲偟偰媮傔傜傟傑偡丅
傛偭偰丄懠偺俀曈偺挿偝偼丄俁乮亖俆亅俀乯丄係乮亖俈亅俁乯偱偡丅
丂倃俀亖俁俀亄係俀
丂倃俀亖俀俆
丂倃亖亇併俀俆
丂倃亖亇俆
丂倃亖俆乮挿偝側偺偱丄倃亜侽乯
丂摎偊丗俆
嘑偙偺栤戣傕摨條偵丄俀揰娫偺嫍棧傪倃偲偡傞偲丄
丂倃傪幬曈偲偡傞捈妏嶰妏宍傪峫偊傞偙偲偑偱偒傑偡丅
偙偺応崌丄懠偺俀曈偺挿偝偼丄偦傟偧傟丄
丂倃嵗昗偺嵎丄倄嵗昗偺嵎偲偟偰媮傔傜傟傑偡丅
傛偭偰丄懠偺俀曈偺挿偝偼丄俁乮亖係亅侾乯丄俁乮亖俈亅係乯偱偡丅
丂倃俀亖俁俀亄俁俀
丂倃俀亖侾俉
丂倃亖亇併侾俉
丂倃亖亇俁併俀
丂倃亖俁併俀乮挿偝側偺偱丄倃亜侽乯
丂摎偊丗俁併俀
婎杮栤戣墘廗偦偺俀
嘆乣嘊偼丄偡傋偰丄俙俛傪幬曈偲偡傞捈妏嶰妏宍偱偡丅
嘆佢俙俛俠亖俁侽亱丄俙俠亖俁們倣偺偲偒丄俙俛偺挿偝傪媮傔傛丅
丂偨偩偟丄俛俠亜俙俠偲偡傞丅
嘇佢俙俛俠亖係俆亱丄俙俛亖係們倣偺偲偒丄俙俠偺挿偝傪媮傔傛丅
嘊佢俙俛俠亖俇侽亱丄俙俛亖俇們倣偺偲偒丄俙俠偺挿偝傪媮傔傛丅
丂偨偩偟丄俛俠亙俙俠偲偡傞丅
夝摎丒夝愢
嘆偙偙偱偼丄侾丗俀丗併俁丂傪巊偄傑偡丅
丂俙俛傪倃偲偡傞偲丄倃偼俀偵奩摉偟傑偡丅乮幬曈偼堦斣挿偄偺偱丅乯
丂俛俠亜俙俠傛傝丄
丂俛俠偼併俁偵丄俙俠偼侾偵奩摉偟傑偡丅
傛偭偰丄
丂倃丗俁亖俀丗侾
丂倃亖俇
丂摎偊丗俇們倣
嘇偙偙偱偼丄侾丗侾丗併俀丂傪巊偄傑偡丅
丂俙俠傪倃偲偡傞偲丄倃偼侾偵奩摉偟傑偡丅乮幬曈偱偼側偄偺偱丅乯
丂俙俛偼丄併俀偵奩摉偟傑偡丅
傛偭偰丄
丂倃丗係亖侾丗併俀
丂倃亖俀併俀
丂摎偊丗俀併俀們倣
嘊偙偙偱偼丄侾丗俀丗併俁丂傪巊偄傑偡丅
丂俙俠傪倃偲偡傞偲丄倃偼併俁偵奩摉偟傑偡丅乮俛俠亙俙俠傛傝乯
丂俙俛偼丄俀偵奩摉偟傑偡丅乮幬曈偱偡偐傜丅乯
傛偭偰丄
丂倃丗俇亖併俁丗俀
丂倃亖俁併俁
丂摎偊丗俁併俁們倣
栤戣墘廗
嘆忋婰偺恾偵偍偄偰丄俙俢亖俆們倣丄俠俢亖侾們倣丄俢俛亖係們倣偺偲偒丄
丂俙俛偺挿偝傪媮傔傛丅
嘇忋婰偺恾偵偍偄偰丄俙俠亖俇們倣丄俛俠亖俁們倣丄佢俛俠俙亖侾俁俆亱偺偲偒丄
丂仮俙俛俠偺柺愊傪媮傔傛丅
嘊掙柺偺敿宎偑俆們倣丄曣慄偺挿偝偑侾俁們倣偺墌偡偄偺懱愊傪媮傔傛丅
嘋柺愊偑俋們倣俀偺惓曽宍偺丄懳妏慄偺挿偝傪媮傔傛丅
嘍侾曈偑俉們倣偺惓嶰妏宍偺丄柺愊傪媮傔傛丅
夝摎丒夝愢
嘆俙俛偺挿偝傪媮傔傞偵偼丄俙俠偲俛俠偺挿偝偑昁梫偱偡丅
丂俛俠偼丄俠俢亄俢俛偱偡偐傜丄俆們倣乮亖侾亄係乯偱偡丅
丂俙俠偼丠
偆傑偄嬶崌偵丄仮俙俠俢偼捈妏嶰妏宍偱丄
俙俢亖俆們倣丄俠俢亖侾們倣偲挿偝傕傢偐偭偰傑偡丅
傑偢丄俙俠傪媮傔傑偟傚偆丅乮俙俠傪倃偲偟傑偡丅乯
丂倃俀亄侾俀亖俆俀
丂倃俀亖俀係
丂倃亖亇併俀係
丂倃亖亇俀併俇
丂倃亖俀併俇丂乮挿偝側偺偱丄倃亜侽乯
傛偭偰丄俙俠偼丄俀併俇們倣
傕偲偵栠偭偰丄崱搙偼仮俙俛俠偵拲栚偱偡丅
偙偙偱偼丄俙俛傪倃偲偟傑偡丅
丂倃俀亖乮俀併俇乯俀亄俆俀
丂倃俀亖係俋
丂倃亖亇併係俋
丂倃亖亇俈
丂倃亖俈丂乮挿偝側偺偱丄倃亜侽乯
傛偭偰丄俙俛偼俈們倣丂偙傟偑丄摎偊偵側傝傑偡丅
嘇嶰妏宍偺柺愊偱偡偐傜丄掙曈偲崅偝偑昁梫偱偡丅
丂掙曈偼丄俛俠偱挿偝傕傢偐傝傑偡偑丄
丂崅偝偵偮偄偰偼丄壓偺恾偺俙俢偑奩摉偟傑偡丅
丂乽掙曈偲崅偝偼捈岎乿偑尨懃偱偡偐傜丄
丂佢俙俢俠亖俋侽亱丄偦偟偰丄
丂佢俙俠俢亖係俆亱乮捈慄侾俉侽亱亅佢俛俠俙乯
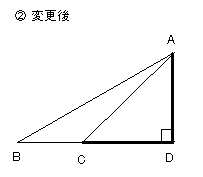
俙俢傪倃偲偡傞偲丄侾丗侾丗併俀偺侾偵奩摉偟傑偡丅
俙俠偼丄侾丗侾丗併俀偺併俀偵奩摉偟傑偡丅
丂倃丗俇亖侾丗併俀
丂併俀倃亖俇
丂倃亖俁併俀
傛偭偰丄俙俢乮崅偝乯偼丄俁併俀們倣
仮俙俛俠偺柺愊偼丄
丂俁亊俁併俀亐俀亖俋併俀乛俀丂們倣俀
嘊墌偡偄偺懱愊傪媮傔傞偨傔偵偼丄
丂掙柺愊偲崅偝偑昁梫偱偡丅
乽掙柺愊乿
掙柺偼丄墌偱偡偐傜丄敿宎亊敿宎亊兾
傛偭偰丄俆亊俆亊兾亖俀俆兾
乽崅偝乿
崅偝傕挿偝偱偡偐傜丄嶰暯曽偺掕棟偱媮傔傑偡丅
曣慄偲丄掙柺偺墌偺敿宎偲丄崅偝偲偱
捈妏嶰妏宍偑峔惉偝傟傑偡丅乮曣慄偑幬曈偵側傝傑偡丅乯
偦傟偧傟丄侾俁們倣丄俆們倣丄倃們倣偲偡傞偲丄
丂倃俀亄俆俀亖侾俁俀
偙傟傪夝偔偲丄
丂倃亖侾俀
乽墌偡偄偺懱愊乿
昁梫側傕偺偑偦傠偄傑偟偨偐傜丄懱愊傪媮傔傑偡丅
丂俀俆兾亊侾俀亐俁亖侾侽侽兾
丂摎偊丗侾侽侽兾丂們倣俁
嘋柺愊偑丄俋們倣俀偺惓曽宍偲偄偆偙偲偼丄
侾曈偑丄俁們倣偲偄偆偙偲偱偡丅
懳妏慄傪幬曈偲偡傞捈妏嶰妏宍傪峫偊傞偲丄
丂倃俀亖俁俀亄俁俀丂乮幬曈偑倃偱偡丅乯
偙傟傪夝偔偲丄
丂倃亖俁併俀
丂摎偊丗俁併俀們倣
乮惓曽宍偵懳妏慄傪傂偔偲丄侾丗侾丟併俀偺捈妏嶰妏宍偑偱偒傑偡丅
丂傕偪傠傫丄偙偪傜偺僷僞乕儞偱夝偄偰傕偐傑偄傑偣傫丅乯
嘍惓嶰妏宍偺俁偮偺妏搙偼丄偡傋偰俇侽亱偱偡偐傜丄
丂侾丗俀丗併俁偑巊偄傗偡偄宍偵側偭偰偄傑偡丅
掙曈偺偪傚偆偳恀拞偐傜丄捀揰偵岦偐偭偰捈慄傪傂偔偲丄
偦傟偑丄乽崅偝乿偵側傝傑偡丅
掙曈偺敿暘偲丄崅偝偲丄幬曈偲偱捈妏嶰妏宍偑偱偒傑偡丅
丂偙偙偱丄掙曈偺敿暘偼丄侾丗俀丗併俁偺侾偵偁偨傝傑偡丅
丂崅偝偼丄侾丗俀丗併俁偺併俁偵偁偨傝傑偡丅
崅偝傪倃偲偡傞偲丄倃丗係亖併俁丗侾
偙傟傪夝偔偲丄倃亖係併俁
暦偐傟偰偄偨偺偼丄惓嶰妏宍偺柺愊偱偡偐傜丄
丂俉亊係併俁亐俀亖侾俇併俁
丂摎偊丗侾俇併俁丂們倣俀
丂巚偭偰偄偨傛傝傕丄挿偔側偭偰偟傑偄傑偟偨丅^^;
丂偙偙偱曗懌偱偡偑丄乽挿偝乿傪暦偐傟偰偄傞応崌偵偼丄
乽嶰暯曽偺掕棟乿偐乽憡帡乮斾乯乿偱丄懳張偱偒傞働乕僗偑傎偲傫偳偱偡丅
乮妎偊偰偍偔偲丄偗偭偙偆栶偵棫偪傑偡丅乯
栚師偵栠傞
堦偮慜乮侾係丏憡帡乯偵栠傞
師乮侾俇丏妋棪乯偵恑傓